关于垛积术的疑惑
这是由于在做一道求极限的运算题引发的,原题要用到求我记得以前学过这个,但那时没有认真对待数学。因此上网查了一下发现要用到这个公式
在网上看了用数学归纳法的证明,知道这个结果的前提下,再用数学归纳法证明是很简单的事情。可是问题是,在看到这个结果之前,他怎么想到这个规律呢?带着这个疑问,我在网上搜了一下。原来我国古代很早就研究过这一类问题,还包括:
,
并总结出了这样的公式。真是厉害啊。他们都用到了叫“垛积术”的方法。目前我没有找到详细的资料,还没有想明白。希望有知道的朋友能介绍点资料。
我看到其中一个思路如下:
[tex] \begin{bmatrix} &n &n& n& n&n\\ & n-1& n-1&n-1 &n-1 \\ &...&...&...&...&... \\ &2& 2& & & \\ &1& && \end{bmatrix}+ \begin{bmatrix} n& n-1& ...& 2&1\\ n& n-1&... &2& \\ ...&...&...&\\ n& n-1& & \\ n& & & \end{bmatrix} + \begin{bmatrix} 1& 2& ...&n-1&n\\ 2& 3&... &n& \\ ...&...&...&\\ n-1& n& & \\ n& & & \end{bmatrix} [/tex]
这样,就形成一个等差数列了。
[tex] \begin{bmatrix}
&2n+1 &2n+1& 2n+1& 2n+1&2n+1\\
&2n+1&2n+1&2n+1 & \\
&...&...& & & \\
&2n+1& 2n+1& & & \\
&2n+1& &&
\end{bmatrix} [/tex]
用等差数列求和公式可得:
[tex]3\sum\limits_{k=1}^n K^2 = (2n+1)\frac{n(n+1)}{2}=\frac{1}{2}n(n+1)(2n+1)[/tex]
从而有:
[tex]\sum\limits_{k=1}^n K^2 = (2n+1)\frac{n(n+1)}{2}=\frac{1}{6}n(n+1)(2n+1)[/tex]
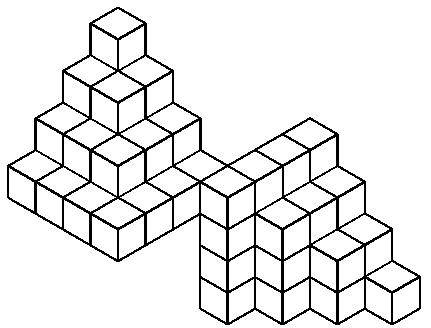
结合垛积术,相当于这里有3堆,先求3堆的总和,然后再除以3,得到结果。我画出了当n=4时,第一堆和第而堆。第三堆,应该是变形才能画出来,图形如下:
可能我的理解有误吧,写出来的目的是希望能有高手指点,或者能有人告诉我,哪里能找到垛积术的详细资料。谢谢!
柯西(Cauchy)收敛准则
当一个数列的极限不是很容易求出来时,那么首要任务就是判断其极限是否存在,只有肯定了极限的存在后,再设法计算其极限。因此柯西收敛准则的重要性不言而喻。
对于这个定理的推导,课本上用到致密性定理,又是看了能看懂,但是自己看之前想不到的感觉,因此记录一下自己的思路。
致密性定理:任一有界数列必有收敛的子序列。
要看数列是否收敛,首先想到有界,这是很自然的,因为如果没有界,则肯定不是收敛的了。但是他怎么就和有界数列的子序列联系起来了呢?致密性定理是柯西收敛准则总结出来就有的吗?柯西也用这个定理来完成他的推理了?
虽然致密性定理相对来说比较简单,而且我的课本上,致密性定理也是在柯西收敛准则之前的。换句话说,当我学完致密性定理后,开始看课本上的柯西收敛准则,然后我在琢磨怎么推导柯西收敛准则时,压根就没有把他和致密性定理想到一块。
我推导过程没有用致密性定理,用了极限的定义和确界定义,似乎也没有漏洞。废话少说,学习笔记如下:
柯西(Cauchy)收敛准则:
数列[tex]\{a_n\}[/tex]有极限 [tex]\Leftrightarrow \forall \varepsilon>0, \exists N \in \mathbf{N}, \forall m,n>N[/tex], 有[tex] \vert x_n - x_m \vert < \varepsilon [/tex]
必要性[tex] \Rightarrow [/tex]: 设[tex] \lim_{x_n \rightarrow \infty} = a [/tex], 则[tex] \forall \varepsilon > 0, \exists N \in \mathbf{N}, \forall k>N [/tex]时,有:
[tex] \vert x_k - a \vert < \frac{\varepsilon}{2} [/tex]
从而可以得到,[tex] \forall m,n>N [/tex],有:
[tex] \vert x_n - x_m \vert = \vert x_n-a+a-x_m \vert \leq \vert x_n-a \vert + \vert a-x_m \vert < \varepsilon [/tex]
有了前面 极限唯一性 和 极限的保序性 的学习,必要性的证明过程再简单不过了。
充分性,既:由[tex] \forall \varepsilon > 0, \exists N \in \mathbf{N}, m,n>N, \vert x_n - x_m \vert < \varepsilon [/tex]得出数列收敛的结论。要看极限是否存在,首先想到判别是否有界,这是很容易想到的了。
当给定一个[tex] \varepsilon [/tex]后,N的值也就确定了,而m,n都是大于N的。由于[tex] \vert x_n-x_m \vert = \vert x_m - x_n \vert [/tex], 因此接下来只讨论[tex]n>m[/tex]的情况就可以了。既然N确定了,不管它有多大,始终都是一个有限值,从有限项[tex] \{\vert x_0 \vert, \vert x_1 \vert, \cdots \vert x_N \vert\} [/tex]取一个最大值都是可以的。于是:记[tex] X=max{ \{\vert x_0 \vert, \vert x_1 \vert, \cdots \vert x_N \vert\}\}[/tex], 而对于这个数列后面可能有无限项,于是是否有界的问题就转化成考察位于N之后的无限项是否有界。由于:
[tex] \vert x_n - x_m \vert < \varepsilon, \forall n>N[/tex], 恒成立,因此取m=N+1,n>m这样做的目的是把每一项都考虑进来,然后考虑那一项最大或最小。由于前面已经考虑了前N项,所以现在从N+1项开始考察。由代数的不等式规则有:
[tex] |x_n| \leq |x_n - x_{N+1}| + |x_{N+1}| < \varepsilon + |x_{N+1}|[/tex]
这就意味着,后面所有的项目都比[tex]|x_{N+1}| + \varepsilon[/tex]要小。于是,界线问题就只需要考虑:[tex] \{X, |x_{N+1}| + \varepsilon\}[/tex]了,对于任意给定的[tex]\varepsilon[/tex],只要[tex]\varepsilon[/tex],那么N以及[tex]|x_{N+1}| + \varepsilon}[/tex]都是可以计算出来的。因此数列有界。
这里课本上假设[tex] \varepsilon = 1 [/tex],然后3,5行就证明出来了,我根据自己的思路在这扯了一通。其实设为任何值都是可以的。
确定有界了,但是有界不一定有极限啊,例如[tex] \{ (-1)^n\}[/tex]有界,但不收敛。然后课本用致密性定理证明了它是有极限的。在看答案之前,我的确想不到。经过了痛苦的挣扎后,我首先想到的是,单调有界数列必有极限。又挣扎之后,我发现根据[tex] \forall \varepsilon>0, \exists N \in \mathbf{N}, \forall m,n>N \vert x_n - x_m \vert < \varepsilon [/tex]
来证明它是单调的,这对我来说似乎很难啊。于是之后,我很自然的想到了有界的定义。主要是第二点:
[tex]\forall \varepsilon > 0, \exists |x_{n0}| \in \{ |x_n| \}, a-\varepsilon < |x_{n0}| [/tex]
这里还是都加个绝对值符号,考虑是上界的情况吧,下界的道理是一样的,不妨设上确界为|a|。
显然,设[tex]|x_k|[/tex]是[tex]\{|x_n|\}[/tex]中最大的,则有:
[tex] \forall \varepsilon > 0, |a|-\frac{\varepsilon}{2}< |x_k| \Rightarrow |x_k|-|a| < \frac{\varepsilon}{2}[/tex]
[tex] \forall m \in \mathbf{N}, |x_m| \leq |x_k| [/tex]
由此有:
1. [tex] |x_m| - |a| < \frac{\varepsilon}{2} \because |x_m| \leq |x_k| [/tex]
由已知:
2. [tex] |x_n| - |x_m| \leq |x_n-x_m| < \frac{\varepsilon}{2} [/tex]
把1和2相加,有:
[tex] |x_n|-|x_m|+|x_m|-|a| < \varepsilon} => |x_n|-|a| < \varepsilon[/tex]
有代数不等式规则有:
[tex] |x_n|-|a| \leq |x_n-a| < \varepsilon[/tex]
从而得到,此数列收敛于[tex]|a|[/tex]。
注意:先睡觉吧!改天再扯!
极限的保序性
已知[tex]\lim_{n \rightarrow \infty} x_n = a, \lim_{n \rightarrow \infty} y_n = b[/tex], 且 [tex]a>b[/tex], 则[tex]\exists N \in \mathbf{N}[/tex],[tex] \forall n>N[/tex],有[tex]x_n > y_n[/tex] 。
课本的证明又一次用选用了[tex]\varepsilon = \frac{a-b}{2}[/tex] !虽然证明过程简单明了,还是老问题,他怎么想到选这个呢?这里就不列出课本的证明了。我的推理如下:
根据极限定义有:
[tex] \left \vert x_n - a \right \vert < \varepsilon [/tex]
[tex] \left \vert y_n - b \right \vert < \varepsilon [/tex]
注意,这里同一个[tex]\varepsilon[/tex]对[tex]a_n[/tex]对应一个[tex]N_1[/tex],对[tex]b_n[/tex]对应一个[tex]N_2[/tex],[tex]N_1[/tex]不一定等于[tex]N_2[/tex]。既:
[tex]{\color{red}{a - \varepsilon}} < x_n < {\color{blue}{a + \varepsilon}}[/tex]
[tex]{\color{blue}{b - \varepsilon}} < y_n < {\color{red}{b + \varepsilon}} [/tex]
由已知条件,[tex]a>b[/tex],因此,一定可以找到一个[tex]\varepsilon > 0[/tex]使得[tex] a-\varepsilon = b+\varepsilon[/tex]成立。既:[tex] \exists \varepsilon > 0 [/tex],有[tex] a-\varepsilon = b+\varepsilon[/tex],可进一步推算出,在此条件下,[tex] a-b = 2\varepsilon[/tex]。
由不等式的递推关系式可进一步得到
[tex] y_n < ({\color{red}{b + \varepsilon}} = {\color{red}{a - \varepsilon}}) < x_n [/tex]
从而得到:
[tex] \exists \varepsilon[/tex],使得 [tex] x_n > y_n [/tex]。
这就可以了吗?实则不然,命题是说[tex]\exists N \in \mathbf{N}[/tex],[tex] \forall n>N[/tex],有[tex]x_n > y_n[/tex] 。而到目前,我们只是证明了以下结论:
[tex] \exists \varepsilon = \frac{a-b}{2} > 0 [/tex],[tex] \exists N_1 \in \mathbf{N}, \exists N_2 \in \mathbf{N} [/tex],有[tex] x_n > y_n [/tex]。
但是对于[tex] n>N_1[/tex]或[tex] n>N_2[/tex]时,[tex]x_n > y_n[/tex]是不是恒成立的,则需要另作讨论。
这时我不禁想到,当[tex] n > N_n[/tex]之后,[tex] y_n [/tex]有没有可能“追上”[tex] x_n [/tex]呢? 不妨再回到前面的那个不等式:
[tex] y_n < ({\color{red}{b + \varepsilon}} = {\color{red}{a - \varepsilon}}) < x_n [/tex]
取[tex]N=Max\{N_1, N_2\}, \varepsilon = \frac{a-b}{2} [/tex],则有:
[tex] \forall n>N, y_n < \frac{a-b}{2} < x_n[/tex]
这就意味着,从[tex]n>N[/tex]以后,所有的[tex]x_n[/tex]都大于[tex]\frac{a-b}{2}[/tex], 所有的[tex]y_n[/tex]都要小于[tex]\frac{a-b}{2}[/tex],因此从这以后[tex] y_n [/tex]就不可能再“追上”[tex] x_n [/tex]了!
最后还是回到了课本上的设 [tex] \varepsilon = \frac{a-b}{2}[/tex],但似乎也知道他为啥要这么设置了!
反过来,若已知数列[tex]\{x_n\}, \{y_n\}[/tex]极限存在,且[tex]\forall n \in \texbf{N}[/tex]有 [tex] x_n \geq y_n [/tex],则有[tex] \lim_{n \rightarrow \infty} x_n \geq \lim_{n \rightarrow \infty} y_n [/tex], 证明方法是一样的。考虑下面这个说明了啥?
[tex] x_n = \frac{n+1}{n}, y_n = \frac{n}{n+1} [/tex] 有:[tex] x_n \geq y_n [/tex] 但:[tex] \lim_{n \rightarrow \infty} x_n = 1 = \lim_{n \rightarrow \infty} y_n[/tex]
[tex] x_n = \frac{1}{n}, y_n = \frac{1}{n+1} [/tex] 有:[tex] x_n \geq y_n [/tex] 但:[tex] \lim_{n \rightarrow \infty} x_n = 0 = \lim_{n \rightarrow \infty} y_n[/tex]
说明了啥?
极限唯一性
若数列[tex]\left \{ x_n \right \}[/tex]的极限存在,则极限值是唯一的。
看了很多数学教材,证明过程都选取了一个[tex] \left \vert a-b \right \vert = \frac{d}{2}[/tex],证明过程虽然简洁明了,而取[tex] \left \vert a-b \right \vert [/tex]也是很容易想到的,但他是怎么想到了个[tex]\frac{d}{2}[/tex]呢?这先给出课本的证明过程,后面是我的推理过程!
设数列[tex]\left \{ x_n \right \}[/tex]有两个不相等的极限值[tex]a[/tex]、[tex]b[/tex],[tex]a \neq b[/tex],则有[tex] d = \left \vert a-b \right \vert > 0[/tex],总可以找到一个正整数[tex]\mathbf{N}[/tex],当[tex]n>\mathbf{N}[/tex]时,总满足下列不等式:
[tex]\left \vert x_n - a \right \vert < \frac{d}{2}[/tex]
[tex]\left \vert x_n - b \right \vert < \frac{d}{2}[/tex]
另一方面有:
[tex] \left \vert a - b \right \vert = \left \vert a - x_n + x_n - b \right \vert = \left \vert (x_n - a) - (x_n - b) \right \vert [/tex]
由代数的不等式公式可得:
[tex] \left \vert (x_n - a) - (x_n - b) \right \vert \leq \left \vert (x_n - a) \right \vert + \left \vert (x_n - b) \right \vert = d[/tex]
即有
[tex] \left \vert a - b \right \vert < d [/tex]
这于假设[tex] d = \left \vert a-b \right \vert > 0[/tex]矛盾,因此极限唯一。
证明过程很简洁明了,可问题是,他怎么就想到在这里,选[tex]\varepsilon = \frac{d}{2}[/tex]呢?这对我来说,总有一种感觉,就是看了别人的能看懂,但是换做自己,则想不到。因此我按我的理解,证明了一下,过程如下:
对于同一个[tex]\varepsilon[/tex],分别有[tex]n1, n2[/tex]根据极限定义有:
[tex]\left \vert x_{n1} - a \right \vert <\varepsilon [/tex]
[tex]\left \vert x_{n1} - b \right \vert < \varepsilon [/tex]
这里n1不一定等于n2,但是根据极限定义,我们取n=Max(n1, n2),从而有:
[tex]{\color{red}{a - \varepsilon}} < x_n < {\color{blue}{a + \varepsilon}}[/tex]
[tex]{\color{blue}{b - \varepsilon}} < x_n < {\color{red}{b + \varepsilon}} [/tex]
由于[tex] a \neq b[/tex],无非有两种情况,[tex] a>b[/tex] 或者 [tex]a<b[/tex],对于[tex] a>b[/tex],由于在极限定义中,[tex]\varepsilon[/tex]是可以任意选取的大于0的数,因此总可以找到一个[tex]\varepsilon[/tex]满足以下条件:
[tex]{\color{red}{a - \varepsilon}} = {\color{red}{b + \varepsilon}}[/tex]
由不等式递推,可得:
[tex]{x_n < (\color{red}{b + \varepsilon}} = {\color{red}{a - \varepsilon}}) < {\color{blue}{x_n}} [/tex]
既得到,[tex] x_n < x_n [/tex],这显然是不可能的,因为对任意自然数[tex]\mathbf{N}[/tex],都有[tex] x_n = x_n [/tex]。
同理对于[tex] a<b[/tex]的情况,总可以找到一个[tex]\varepsilon>0[/tex]满足以下条件:
[tex]{\color{blue}{b - \varepsilon}} = {\color{blue}{a + \varepsilon}}[/tex]
也得到,[tex] x_n < x_n [/tex]的结论。因此无论[tex]a<b[/tex]还是[tex]a>[/tex]的情况,都可以找到一个反例子。所以假设不成立。推理到这里,我终于理解课本要选取[tex]\varepsilon = \frac{d}{2}[/tex]了。
我的推理过程应该也没有漏洞吧,:)