这是由于在做一道求极限的运算题引发的，原题要用到求我记得以前学过这个，但那时没有认真对待数学。因此上网查了一下发现要用到这个公式在网上看了用数学归纳法的证明，知道这个结果的前提下，再用数学归纳法证明是很简单的事情。可是问题是，在看到这个结果之前，他怎么想到这个规律呢？带着这个疑问，我在网上搜了一下。原来我国古代很早就研究过这一类问题，还包括：, 并总结出了这样的公式。真是厉害啊。他们都用到了叫“垛积术”的方法。目前我没有找到详细的资料，还没有想明白。希望有知道的朋友能介绍点资料。

我看到其中一个思路如下：

[tex] \begin{bmatrix} &n &n& n& n&n\\ & n-1& n-1&n-1 &n-1 \\ &...&...&...&...&... \\ &2& 2& & & \\ &1& && \end{bmatrix}+ \begin{bmatrix} n& n-1& ...& 2&1\\ n& n-1&... &2& \\ ...&...&...&\\ n& n-1& & \\ n& & & \end{bmatrix} + \begin{bmatrix} 1& 2& ...&n-1&n\\ 2& 3&... &n& \\ ...&...&...&\\ n-1& n& & \\ n& & & \end{bmatrix} [/tex]

这样，就形成一个等差数列了。

[tex] \begin{bmatrix}
&2n+1 &2n+1&  2n+1& 2n+1&2n+1\\
&2n+1&2n+1&2n+1  & \\
&...&...& & &  \\
&2n+1& 2n+1&  & & \\
&2n+1&  &&
\end{bmatrix} [/tex]

用等差数列求和公式可得:

[tex]3\sum\limits_{k=1}^n K^2 = (2n+1)\frac{n(n+1)}{2}=\frac{1}{2}n(n+1)(2n+1)[/tex]

从而有：

[tex]\sum\limits_{k=1}^n K^2 = (2n+1)\frac{n(n+1)}{2}=\frac{1}{6}n(n+1)(2n+1)[/tex]

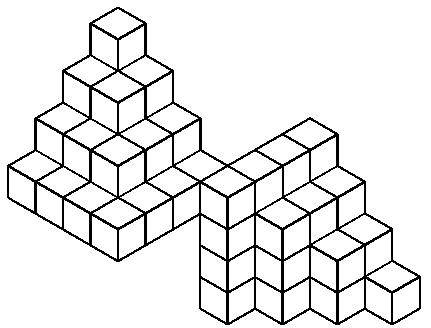
结合垛积术，相当于这里有3堆，先求3堆的总和，然后再除以3，得到结果。我画出了当n=4时，第一堆和第而堆。第三堆，应该是变形才能画出来，图形如下：

可能我的理解有误吧，写出来的目的是希望能有高手指点，或者能有人告诉我，哪里能找到垛积术的详细资料。谢谢！